子集(78)
今天是小浩算法 “365刷题计划” 第105天。这是昨天一个同学面试快手被问到的算法题,很不幸的是他被挂掉了。征得对方同意后,拿出来分享给大家~

01、题目示例
子集:如果集合A的任意一个元素都是集合B的元素,那么集合A称为集合B的子集。
| 第48题:子集 |
|---|
| 给定一组不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。 |
说明: 解集不能包含重复的子集
示例:
输入: nums = [1,2,3]输出: [ [3], [1], [2], [1,2,3], [1,3], [2,3], [1,2], [] ]
题目本身没有太多需要补充的,初中数学知识:

02、题解分析(高级)
上一个很厉害的题解。
首先我们可以证明一下 N 个元素的子集个数有 2^N 个:

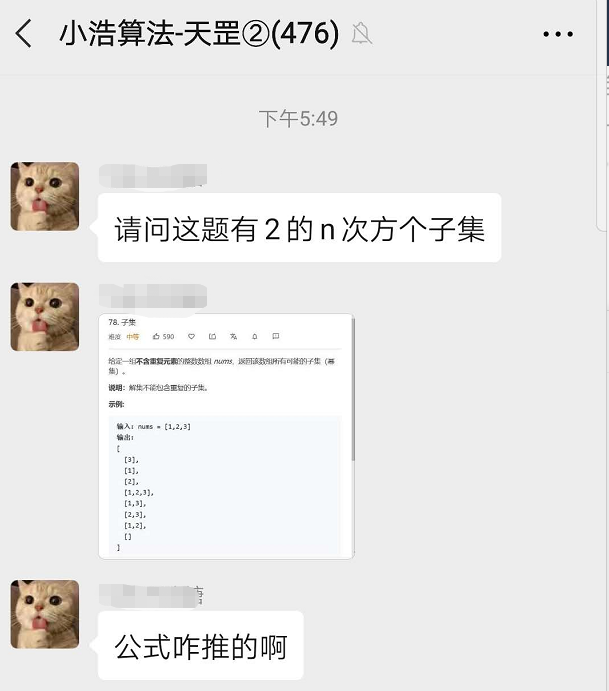
可以类比为 N 个不同的小球,一次拿出若干个小球(可以不拿),对于每一个球都可以选择拿或者不拿,共有 N 个球,总共判断 N 次,产生了 2^N 个子集。比如:123,共有下面 8 个子集:
然后考虑解题思路,暂且不谈回溯,我们其实可以用二进制来模拟每个元素是否选中的状态。 又因为我们已知了对于 N 个元素共有 2^N 个子集,所以我们直接遍历 2^N 个元素。
class Solution {public List<List<Integer>> subsets(int[] nums) {//存放所有子集List<List<Integer>> res = new ArrayList<>();//子集总数共有 2^N 个int length = 1 << nums.length;//遍历所有的子集for (int i = 0; i < length; i++) {List<Integer> sub = new ArrayList<>();//TODO : 找到对应的子集元素}return res;}}
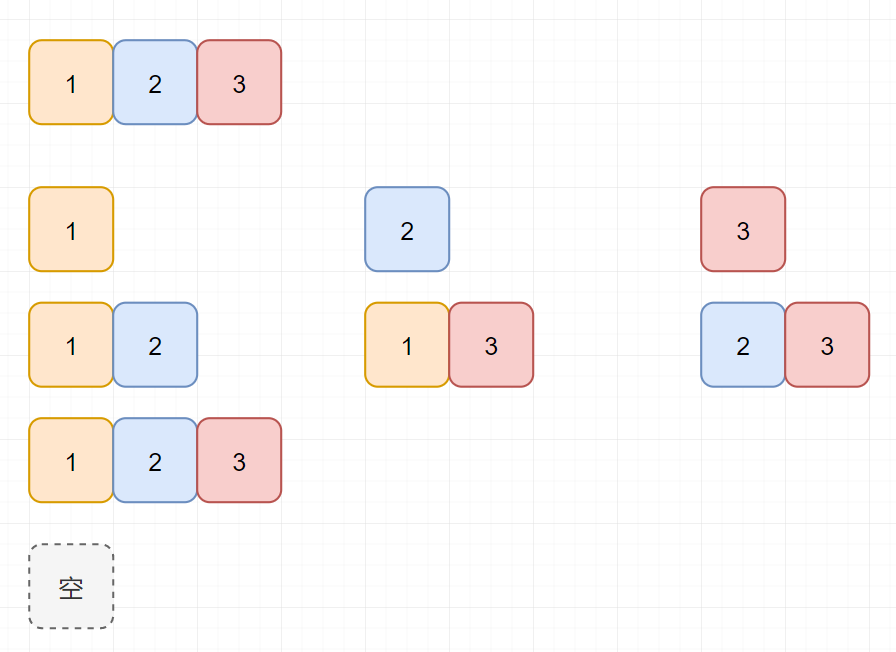
但是我们并不知道具体的子集元素。那如何找到对应的子集元素呢?对于 2^N 个 N 位的二进制数,我们可以通过从后往前的第 j 个二进制位的 0 和 1 来表示是否放入子集集合。
for (int j = 0; j < nums.length; j++) {if (((i >> j) & 1) == 1) sub.add(nums[j]);}
综合一下代码:
class Solution {public List<List<Integer>> subsets(int[] nums) {//存放所有子集List<List<Integer>> res = new ArrayList<>();//子集总数公有 2^N 个int length = 1 << nums.length;//遍历所有的子集for (int i = 0; i < length; i++) {List<Integer> sub = new ArrayList<>();for (int j = 0; j < nums.length; j++) {if (((i >> j) & 1) == 1) sub.add(nums[j]);}res.add(sub);}return res;}}
为帮助大家理解,假设 nums 为 [1,2,3],res 的存储过程为:
大家可以仔细体会一下这个题解。

03、题解分析(普通)
当然,上面的题解并不是凡人可以直接想到的。所以我们这里还是给出一种更为通用的题解~
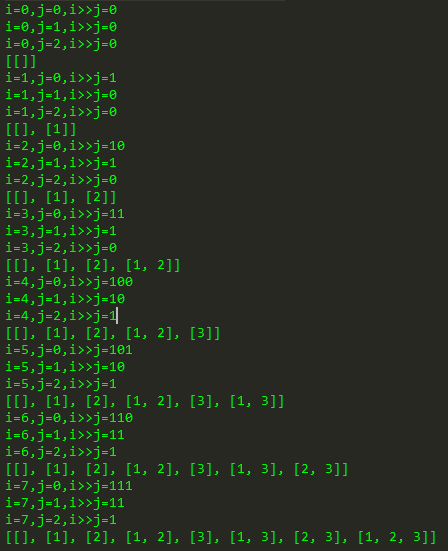
集合中所有元素的选/不选,其实构成了一个满二叉树。左子树选,右子树不选。自然,那从根节点到所有叶子节点的路径,就构成了所有的子集。
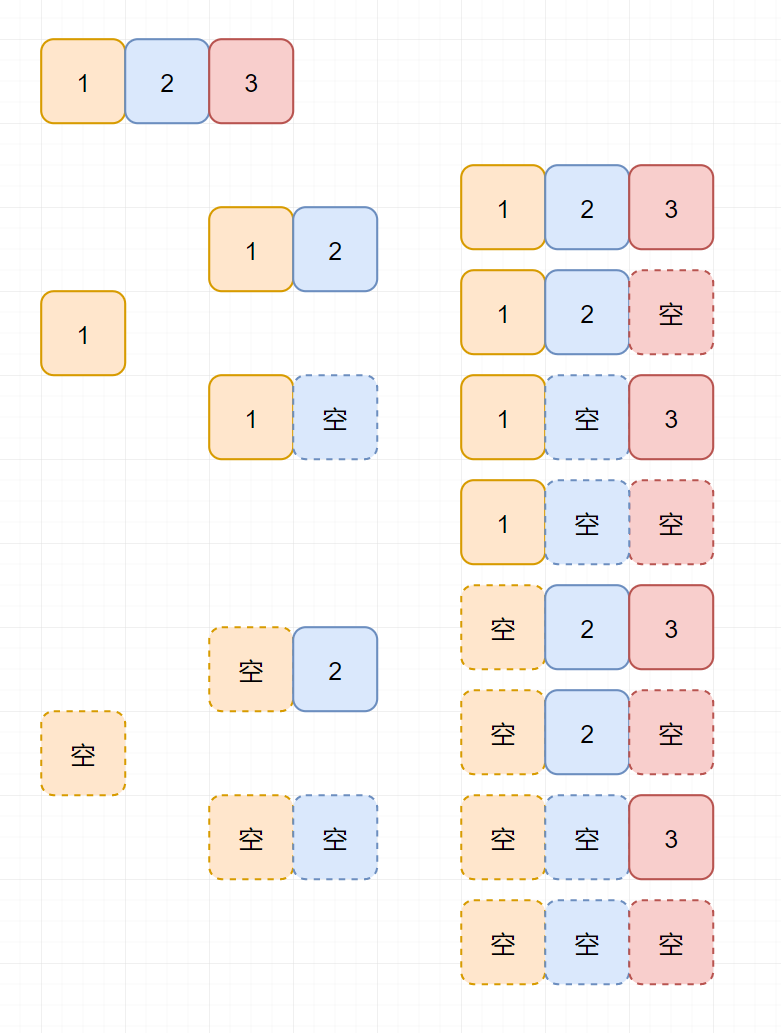
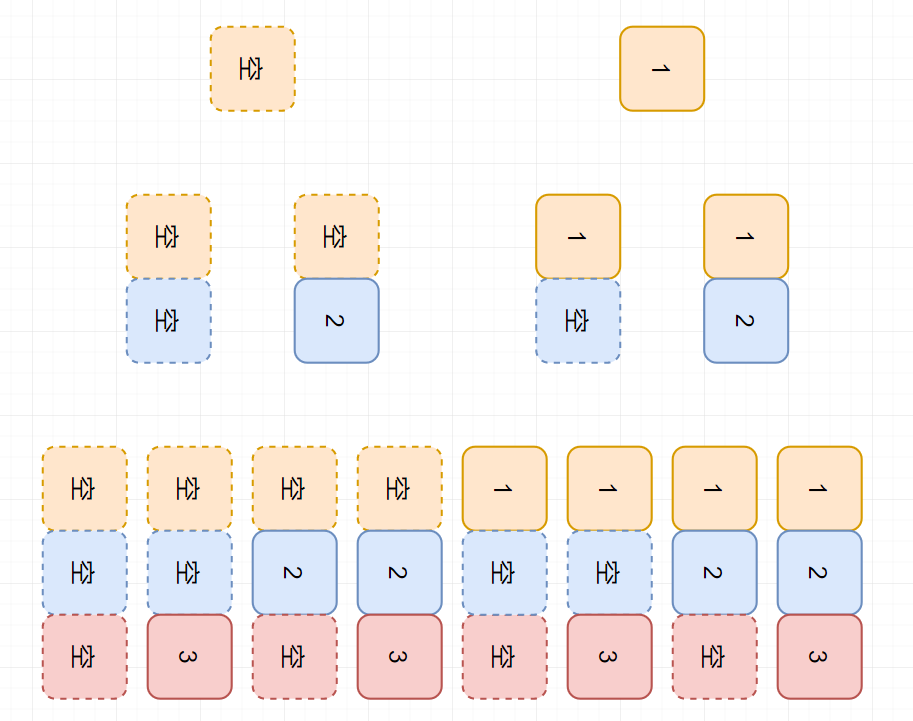
那这种解法其实就好理解很多了:
class Solution {List<List<Integer>> res;public List<List<Integer>> subsets(int[] nums) {res = new ArrayList<>();List<Integer> list = new ArrayList<>();dfs(nums, 0, list);return res;10 }private void dfs(int[] nums, int start, List<Integer> list) {for (int i = start; i < nums.length; i++) {list.add(nums[i]);dfs(nums, i + 1, list);list.remove(list.size() - 1);}res.add(new ArrayList<>(list));}}
总之,这道题目其实还是有一定难度的,难点主要包括:
- 数学知识的混淆,忘记考虑空集等情况。
- 和全排列问题混淆,把 2^N 当做 N!处理。
- 递归与回溯细节掌握不扎实。
但并不是不可以攻克,建议大家下去自行练习一番~
加油,奥利给!
