-
整数拆分(343)
能跟着看到现在,大家都有点疲惫了。为了提高各位积极性,我打算每天在文首放一张女神的图(不为别的,只为激励大家,毕竟美女对男女都是通杀的。祝大家早日拿到理想offer,实现人生赢家)话不多说,直接看题!
01、题目示例
这两天越来越多的读者私信小浩,说觉得只看题的话,不是很系统,想让我系统的讲一讲各类数据结构。对于这个问题,我统一回复一下,首先后面肯定是有系统的讲解各类数据结构的打算的,这个目前正在筹划中,所以大家请放心!另外对于看题,如果担心缺乏基础知识看不懂的朋友们,大家请一万个放心。老读者都知道,我讲题,一般都是会把这个题涉及到的基础知识都给你过一遍的。当然后面我也会用系列篇,把这些题目再串起来,所以大家还是耐心点的去看。记住,干就对了!
| 第343题:整数拆分 |
|---|
| 给定一个正整数 n,将其拆分为至少两个正整数的和,并使这些整数的乘积最大化。返回你可以获得的最大乘积。 |
示例 1:
输入: 2输出: 1解释: 2 = 1 1, 1 × 1 = 1。
示例 2:
输入: 10输出: 36解释: 10 = 3 3 4, 3 × 3 × 4 = 36。
说明: 你可以假设 n 不小于 2 且不大于 58。
02、题目分析
这个题理解了题意的话,其实还是比较简单的,一起看下。
要对一个整数进行拆分,并且要使这些拆分完后的因子的乘积最大。我们可以先尝试拆分几个数值,测试一下。
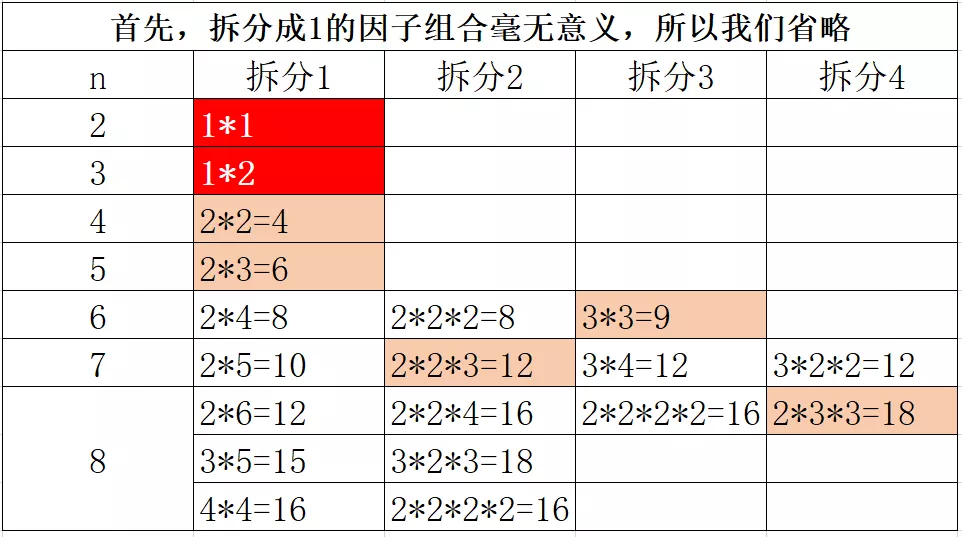
通过观察,首先肯定可以明确,2 和 3 是没办法进行拆分的最小因子。同时,我们好像能看出来:
- 只要把 n 尽可能的拆分成包含3的组合,就可以得到最大值。
- 如果没办法拆成 3 的组合,就退一步拆成 2 的组合。
- 对于 3 和 2 ,没办法再进行拆分。
根据分析,我们尝试使用贪心进行求解。因为一个数(假设为n)除以另一个数,总是包括整数部分(x)和余数部分(y)。那刚才也得到了,最优因子是3,所以我们需要让 n/3,这样的话,余数可能是 1,2 两种可能性。
- 如果余数是 1 ,刚才我们也分析过,对于 1 的拆分是没有意义的,所以我们退一步,将最后一次的 3 和 1 的拆分,用 2 和 2 代替。
- 如果余数是 2 ,那不消多说,直接乘以最后的 2 即可。
根据分析,得出代码:
//JAVApublic static int integerBreak(int n) {if (n <= 3) return n - 1;int x = n / 3, y = n % 3;//恰好整除,直接为3^xif (y == 0) return (int) Math.pow(3, x);//余数为1,退一步 3^(x-1)*2*2if (y == 1) return (int) Math.pow(3, x - 1) * 4;//余数为2,直接乘以2return (int) Math.pow(3, x) * 2;}
03、证明过程
答案是碰出来了,但是我们是通过观察,发现最优因子应该是 3 。那如何来证明这个结论的正确性呢?
首先,通过均值不等式,很容易验证当每一个拆分值都相等的时候,才具有最大值,所以实际上就是将这个数均分。那么,对于整数,我们将其分解成
份,每一份为
则有
求的极值点为
,最接近的也就是 3 了。(注意:这里是整数,如果是实数,该证明则有漏洞)
04、都看不懂
一力破万法,乱拳打死老师傅,使用万能的动态规划求解。
dp[i]代表 i 拆分之后得到的乘积的最大的元素,比如dp[4]就保存将4拆分后得到的最大的乘积。状态转移方程式为
dp[i]=max(dp[i],(i-j)*max(dp[j],j))
整体思路就是这样,将一个大的问题,分解成一个一个的小问题,然后完成一个自底向上的过程。举一个例子,比如计算 10 ,可以拆分 6 和 4 ,因为 6 的最大值 3x3,以及 4 的最大值 2x2 都已经得到,所以就替换成 9 和 4 ,也就是 10=3x3x4。
代码如下:(CPP听说很受欢迎?)
//Cclass Solution {public:int integerBreak(int n){vector<int> dp(n 1, 0);dp[1] = 1;for (int i = 2; i <= n; i ){for (int j = 1; j < i; j ){dp[i] = max(dp[i], max(dp[j], j) * (i - j));}}return(dp[n]);}};
今天的题目可能有一定难度,建议大家自己写写画画,才能真正的做到理解和巩固。
